Maksimalaus srauto konstravimas

Didinančiosios grandinės

Kurie grafo lankai yra suderinti, o kurie - nesuderinti?

Didinančiosios grandinės

Suderinti: $(1, 2), (1, 4), (2, 3), (2, 5), (3, 6), (5, 6)$. Nesuderinti: $(4, 5)$

Didinančiosios grandinės

• Ilgio $l$ didinančioji grandinė iš $s$ į $t$ srauto $f$ atžvilgiu yra seka, sudaryta iš besikeičiančia tvarka surašytų viršūnių ir lankų: $$v_0, e_1, v_1, e_2, v_2, ..., v_{l-1}, e_l, v_l.$$
• Čia $v_1=s$, $v_l=t$ ir $\forall 1 \leq i \leq l$ lankas $e_i$ srauto $f$ atžvilgiu yra leistinasis lankas iš $v_{i-1}$ į $v_i$.

Didinančiosios grandinės

Raskite didinančiąsias grandines šiame grafe.

Didinančiosios grandinės

$1, (1,2), 2, (2,3), 3, (3,6), 6$ ir $1, (1,2), 2, (2,5), 5, (5,6), 6$.

Didinančiosios grandinės

Raskite didinančiąsias grandines šiame grafe.

Didinančiosios grandinės

$1, (1, 3), 3, (3, 5), 5, (5, 2), 2, (2, 4), 4, (4, 6), 6$.

Didinančiosios grandinės

• Žinodami tam tikrą didinančią grandinę, srautą $f$ galime padidinti dydžiu $\delta = \min \{\Delta(e_i), 1 \leq i \leq l\}$.
• Jei $e_i$ yra suderintasis lankas, tai $\Delta(e_i)=c(e_i)-f(e_i)$.
• Jei $e_i$ yra nesuderintasis lankas, tai $\Delta(e_i)=f(e_i)$.
• Žinodami reikšmę $\delta$ konkrečiai didinančiai grandinei, galime šį dydį pridėti prie kiekvieno šios grandinės lanku tekančio srauto (jei lankas nesuderintasis - reikia atimti).

Didinančiosios grandinės

Kodėl naujai apskaičiuota funkcija $f'$ vis dar yra srautas? Nesunku įsitikinti, kad vis dar galios sąlyga $0 \leq f'(e) \leq c(e)$. Panagrinėkime, kaip keičiasi divergencija.

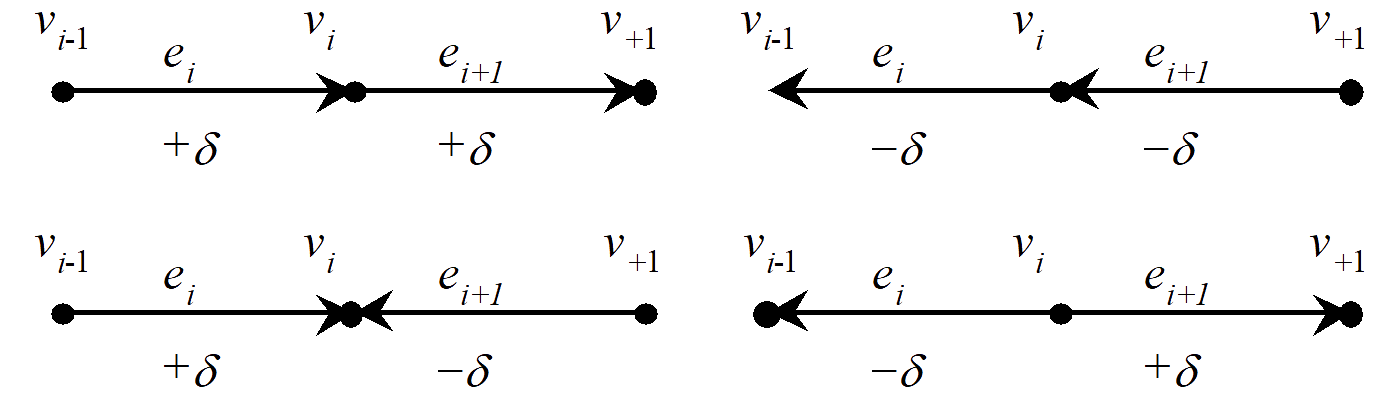
Didinančiosios grandinės

Padidinkite srautą didinančiojoje grandinėje $1, (1,2), 2, (2,3), 3, (3,6), 6$.

Didinančiosios grandinės

$\delta=\min \{ 6-1, 1-0, 2-0 \} = \{ 5, 1, 2 \} = 1$. Padidinus srautą grafas atrodo taip:

Įrodymas $1 \Rightarrow 2$

• Jei srautas maksimalus, tai didinanti grandinė niekaip negali egzistuoti.
• Jei didinanti grandinė egzistuotų, tai ja pasinaudojus būtų galima padidinti srautą, bet tai reikštų, kad srautas nebuvo maksimalus.

Įrodymas $2 \Rightarrow 3$

• Tarkime, kad srautui $f$ neegzistuoja didančiosios grandinės.
• Tegu $A$ - viršūnių aibė, kurią sudaro visos viršūnės, iki kurių egzistuoja grandinė iš $s$, einanti tik per leistinus lankus.
• Šiai aibei tikrai priklauso $s$ ir tikrai nepriklauso $t$ (nes kitaip egzistuotų didinanti grandinė).
• Kiekvienam pjūvio suderintam lankui privalo galioti lygybė $f(e) = c(e)$, nes kitaip būtų galima praplėsti aibę $A$. Todėl $f(A, V \setminus A) = c(A, V \setminus A)$.
• Analogiškai, kiekvienam pjūvio nesuderintam lankui privalo galioti lygybė $f(e) = 0$. Todėl $f(V \setminus A, A) = 0$.
• Iš čia $W(f) = f(A, V \setminus A) - f(V \setminus A, A) = c(A, V \setminus A)$.

Įrodymas $3 \Rightarrow 1$

• Srauto dydis negali viršyti $c(A, V \setminus A)$.
• Kadangi $W(f) = c(A, V \setminus A)$, tai srautas $f$ yra maksimalus.

Užduotis

Raskite maksimalų srautą duotame grafe pasitelkę Ford-Fulkerson algoritmą.

Atsakymas

Maksimalus srautas: $11$.

Ar algoritmas visada baigia darbą?

• Viskas priklauso nuo to, kaip bus renkamos didinančios grandinės.
• Yra įrodyta, kad egzistuoja tinklų, kuriuose galima taip parinkinėti grandines, kad procesas niekada nesibaigs. Tačiau praktikoje tokių atvejų beveik nepasitaiko.
• Edmonds'as ir Karp'as įrodė, kad parinkinėjant didinančias grandines paieškos į plotį tvarka (t.y. renkant mažiausiai lankų turinčias grandines), algoritmas visada baigs darbą ir maksimalus srautas bus sukonstruotas per ne daugiau kaip $\frac{mn}{2}$ grandinių.